What is a proof system?

I wonder if you can relate to this. When I first encountered Zero Knowledge Proofs (ZKPs), I had to work through reams and reams of papers, articles, and videos to finally “get it.” It isn’t hard to see why — the terminology and acronyms become pretty intimidating. Even when I finally understood “IP,” “PCP,” “IOP,” and “MIP,” it still wasn’t clear how they fit into the larger picture.
Now that I have a handle on ZKPs, I think I can save you a lot of time. You can think of this post as a primer to ZKPs, so when you go down the rabbit hole, you won’t feel quite as lost as I did.
We’ll start with an overview of the basic parts of a proof system. Then, we’ll delve into the evolution of proof systems and the various assumptions they make. After that, we’ll look at different models of proof systems before we end with an overview of how the most popular proof systems are currently modeled.
What’s a Proof System?
In computer science, a “proof” is a formal demonstration that a particular statement is true. Proofs are formalized using “proof systems.” We can break proof systems into five major pieces:
1) Formal Language
Proof systems convey statements and properties through a formal language, which you can think of as a precise and standardized syntax for writing formulas and expressing assertions. This includes logical connectives, quantifiers, variables, and other symbols.
2) Axioms
Axioms are basic truths or assumptions that are accepted as true without a proof. They serve as the starting point for constructing proofs.
3) Inference Rules
Inference rules define how one statement can be transformed into another following the principles of logic.
4) Proof Derivation
To derive a proof, we start from the axioms and use inference rules to derive new statements from preceding statements until we arrive at the final assertion. This step-by-step derivation of statements, then, brings us to our final assertion.
5) Soundness and Completeness
Soundness says that if a statement is proven within the system, it’s true. Completeness guarantees that if a statement is true, it’s provable within the system. So, soundness guarantees that proof systems don’t produce false results, while completeness ensures that true statements are accepted within the proof system.
The Evolution of Proof Systems
Now that you have a basic vocabulary of proof systems, let’s take a look at how they’ve evolved over the last 30 years. We’ll use a classic computer science problem, the graph coloring problem, to understand how a person (i.e., the prover) would prove their solution to another person (i.e., the verifier) using each system.
The graph coloring problem is pretty straightforward. Given an undirected graph, the objective is to assign colors to its vertices such that no two adjacent vertices share the same color.

Let's see how the following proof systems approach the graph coloring problem.
Nondeterministic Polynomial-time (“NP”)
First up, let’s take a look at the classic mathematical proof known as “nondeterministic polynomial-time” (NP). If a problem is NP, it means a polynomial-time algorithm or proof system exists that can check if the efficient solution is correct. In other words, NP defines the set of problems for which efficient solutions exist, and proof systems provide us with a framework for checking the validity of solutions for such problems.
But let’s see that in action. How would we generate an NP proof for the graph coloring problem?
In this case, the prover simply provides a potential coloring assignment for the graph, and the verifier checks its validity by verifying all the vertices and ensuring no two adjacent vertices have the same color. That’s it!

Interactive Proof (IP)
In 1985, Goldweisser and Micali introduced a revolutionary idea: a “prover” and “verifier” can interact to verify the validity of a statement. This idea of an interactive proof (IP) was so influential that, decades later, they won the Turing Award (2012).
It’s pretty simple. First, the prover tries to convince the verifier of the correctness of a statement. The verifier challenges the prover with a series of “random” questions. The prover responds. This happens for many rounds until the verifier is convinced that the prover’s statement is true.
Most importantly, IP lets us use probabilistic verification. For instance, over many rounds, the prover can convince the verifier with a high probability that she is being honest. So, IP is probabilistic, as opposed to a classical mathematical proof, which is deterministic.
Using interaction and randomness, IPs let us build proof systems where the prover has privacy. In other words, the prover can prove her statement without revealing anything about the statement (in other words, it’s “zero knowledge”).
How would we generate an IP proof for the graph coloring problem?
In this case, the verifier would start by randomly selecting a subset of vertices and asking the prover to provide the colors assigned to those vertices. The verifier then verifies the correctness of the colors assigned to the selected vertices and checks that no two adjacent vertices share the same color. The verifier continues to select a random set of vertices and ask the prover for their colors over several rounds until he gains high confidence that the prover knows the solution.
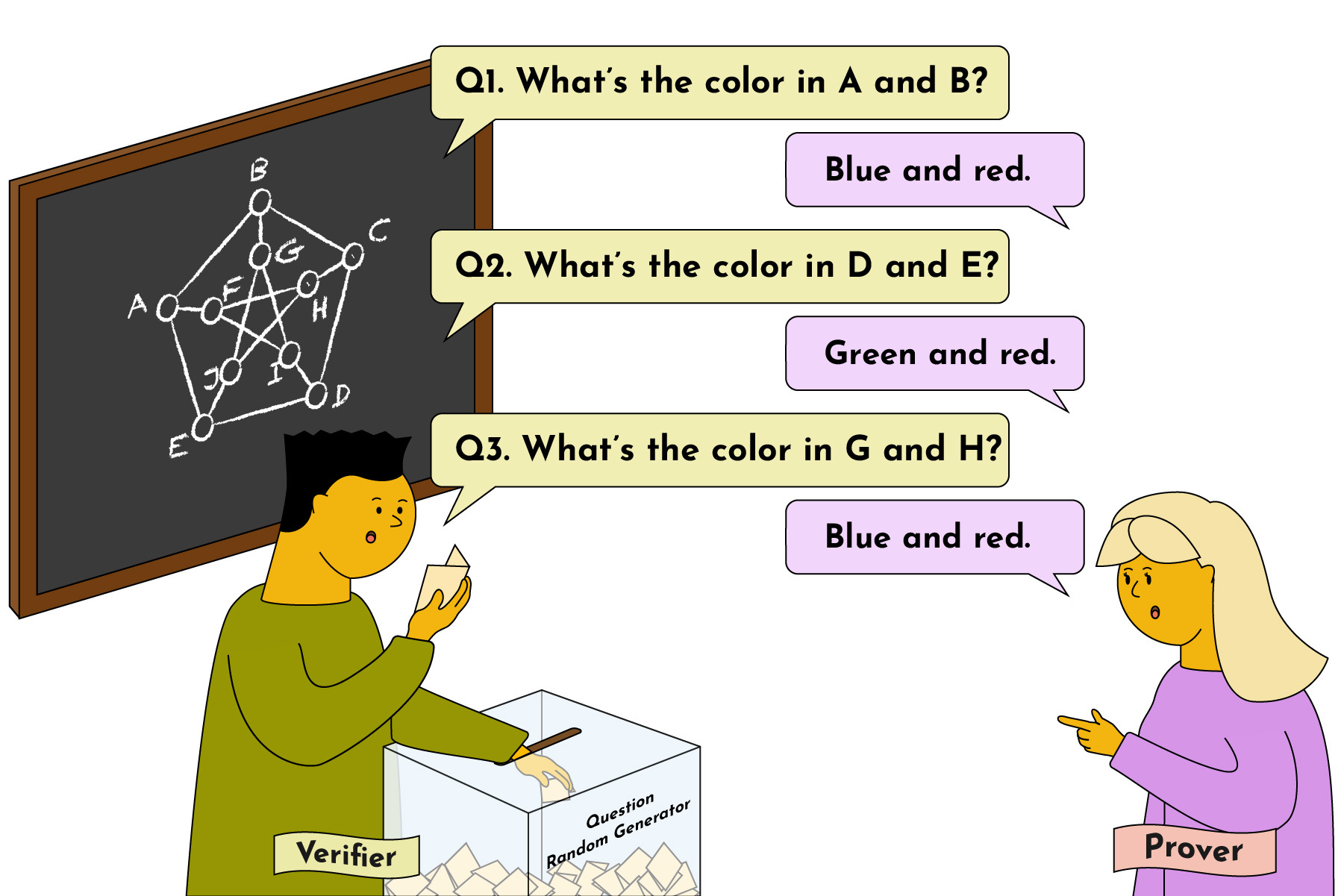
Probabilistic Checkable Proofs (PCP)
A probabilistic checkable proof (PCP) is another evolution of the classical NP proof system. The key difference? It isn’t interactive. Instead, with PCP, a proof is transformed into a fixed-size format called a "proof transcript." The verifier can randomly query a small number of bits in the transcript to verify the proof.
A “random oracle” gives PCP the ability to query the proof transcript randomly! That way, the prover can’t predict queries ahead of time. In the case of PCPs, when we say we have access to a “random oracle”, it means we have access to the proof transcript and a source of randomness such that the verifier can access random parts of the proof transcript.
Overall, PCPs are pedagogically useful — but they aren’t efficient in practice because the proofs are large and query complexity is high.
So how would we generate a PCP proof for the Graph Coloring problem?
The prover constructs a proof transcript that encodes the coloring assignment. The verifier queries for the vertices of the graph using the randomness provided by the oracle, and gets access to the color at those vertices via the oracle. Based on the results of the queries, the verifier can choose to either accept or not accept. Note that there is NO interaction in this case. The prover simply generates the proof transcript once, and the verifier uses random queries via the oracle to validate the proof.

Interactive Oracle Proof (IOP)
The next historical milestone is the interactive oracle proof (IOP), which is an extension of the interactive proof idea, except it also incorporates random oracles (like in PCP). So, in an IOP, the prover and the verifier interact with one another and have access to random oracles. IOPs make interactive proofs more efficient by using oracles to reduce communication and query complexity. This is the model that state-of-the-art zero-knowledge proofs use!
So how would we generate an IOP proof for the graph coloring problem?
Similar to PCP, the prover constructs a proof transcript that encodes the coloring assignment, and the verifier queries for the vertices of the graph randomly using the oracle. The oracle gives the verifier access to the color at those queried vertices. But rather than sending the entire proof transcript at once, as with PCPs (which is inefficient), IOP breaks it up and sends small parts of it over multiple interactions until the verifier is convinced the prover knows the solution.

Summary
Phew. That was a lot of information! Before we move on, let’s quickly summarize the past few sections:
- IP = A proof system with Interaction + Randomness
- PCP = A proof system with Randomness + Oracle Access
- IOP = A proof system with Interaction + Randomness + Oracle Access

Note: For the sake of simplicity, I left out “MIP” and “MIOP,” which are essentially the same as IP and IOP except with multiple isolated provers. These models have attractive features, such as space efficiency, but are tricky and not widely used.
Proof System + Cryptography = SNARKS / STARKS
We can break down zkSNARKs and zkSTARKs into two components: Information-theoretic proof systems and cryptographic compilers.
Information-Theoretic Proof System
We learned about different proof systems in the previous section. “Information-theoretic” refers to the proof system’s ability to provide soundness and completeness even against adversaries with unbounded computational power. So an Information-Theoretic proof system makes idealized assumptions that are difficult to enforce in real life. For instance, it may assume that the verifier is trusted and has restricted access to the proof.
Because an information-theoretic proof system doesn’t care about how this assumption is managed in the real world, it’s useless as a standalone object. However, it can become useful if it’s combined with a cryptographic compiler, as you’ll see next.
Cryptographic Compiler
The cryptographic compiler removes the idealized assumptions that the information-theoretic proof system makes. How? By using cryptographic primitives, such as a collision-resistant hash function, a random oracle, or a generic bilinear group.
The output is a real-world proof system that’s only secure under a computationally bounded prover and/or verifier (this is an assumption that all cryptographic protocols make).
The cryptographic compiler can also provide other desirable properties to the information-theoretic proof system, such as eliminating interaction, reducing communication complexity, or adding a zero-knowledge feature.
Why the Separation?
But wait. If one isn’t useful without the other, then why are they separated? The answer is modularity. By keeping the system modular, we can analyze, optimize, and implement each part separately.
For instance, in the information-theoretic proof system, we can optimize it based on information theory principles. We can then use different cryptographic compilers on a specific information theoretic proof system to obtain different real-world proof systems, each with its own tradeoff in efficiency, security, and trusted setup assumptions.
Moreover, information-theoretic protocols serve as cleaner objects of study than the final real-world proof system after it has been compiled using a cryptographic compiler.
Conclusion
Great work making it to the end! We covered a lot of ground here, from defining the five elements of proof systems to differentiating proof systems based on their properties, such as interaction, randomness, or oracle access. If this feels all too confusing still, that’s okay. Just come back to it and read it again and again. Eventually, it will make sense.
As you dive further into the world of ZKPs, hopefully, you’ll find that the time you spent here saved you from some toil!
